

Sometimes this will be faster with multiplication by -1, which will require us to switch the direction of the inequality symbol.įor example, let’s say we have the quadratic inequality -2x 2 + 3x + 4 > 5. However, we want to take the extra step of making a > 0 (that is, a positive coefficient for x 2). Standard form just means that one side of the inequality is zero. Convert The Quadratic Inequality To Standard Form With a > 0 Then, we’ll look at some examples to make things clear. Shade the appropriate region on the graph, based on the inequality sign.įirst, we’ll explain each of these steps in more detail. Graph the parabola corresponding to the quadratic. Write the solution set for the quadratic inequality. Use v y to identify the case for the solutions. Find the value of v y (the y-coordinate of the vertex of the parabola). Convert the quadratic inequality to standard form with a > 0. Doing them in this order ensures that you won’t miss anything along the way:

There are 7 steps to take if you want to solve and graph a quadratic inequality.
#QUADRATIC INEQUALITIES HOW TO#
How To Solve & Graph Quadratic Inequalities We’ll pay special attention to the possible cases for the solution sets and what to do in each situation. In this article, we’ll take a closer look at the steps to solve and graph quadratic inequalities. Of course, some cases are easier to solve and graph than others, but there is a way to do every problem. Finally, shade the appropriate region on the graph based on signs and the inequality symbol. Then, graph the corresponding parabola from the quadratic. Next, identify the case you are in, and find the zeros of the quadratic. So, how do you solve & graph quadratic inequalities? To solve a quadratic inequality, first convert it to standard form. However, if you have a method, you can solve these problems without much trouble. Solving and graphing quadratic equations is one thing, but quadratic inequalities add another layer of work to be done. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License. We recommend using aĪuthors: Lynn Marecek, Andrea Honeycutt Mathis Use the information below to generate a citation. Then you must include on every digital page view the following attribution: If you are redistributing all or part of this book in a digital format, Then you must include on every physical page the following attribution: If you are redistributing all or part of this book in a print format, Want to cite, share, or modify this book? This book uses the In the next example, the quadratic inequality solutions will result from the solution of the quadratic equation being complex. Using the Quadratic Formula to solve the quadratic equation, the radicand is a negative. The last row of the table shows us when the parabolas never intersect the x-axis. This correlates to our previous discussion of the number and type of solutions to a quadratic equation using the discriminant.įor a quadratic equation of the form ax 2 + bx + c = 0, a ≠ 0. These two solutions then gave us either the two x-intercepts for the graph or the two critical points to divide the number line into intervals. This resulted from the fact that, in each case we found two solutions to the corresponding quadratic equation ax 2 + bx + c = 0. The solutions of the quadratic inequalities in each of the previous examples, were either an interval or the union of two intervals. Solve − x 2 + 8 x − 14 < 0 − x 2 + 8 x − 14 < 0 algebraically. − x 2 + 6 x − 7 ≥ 0 − x 2 + 6 x − 7 ≥ 0 in the middle interval Then substitute in the values of a, b, c a, b, c. X = − b ± b 2 − 4 a c 2 a x = − b ± b 2 − 4 a c 2 a Multiply both sides of the inequality by −1 −1.
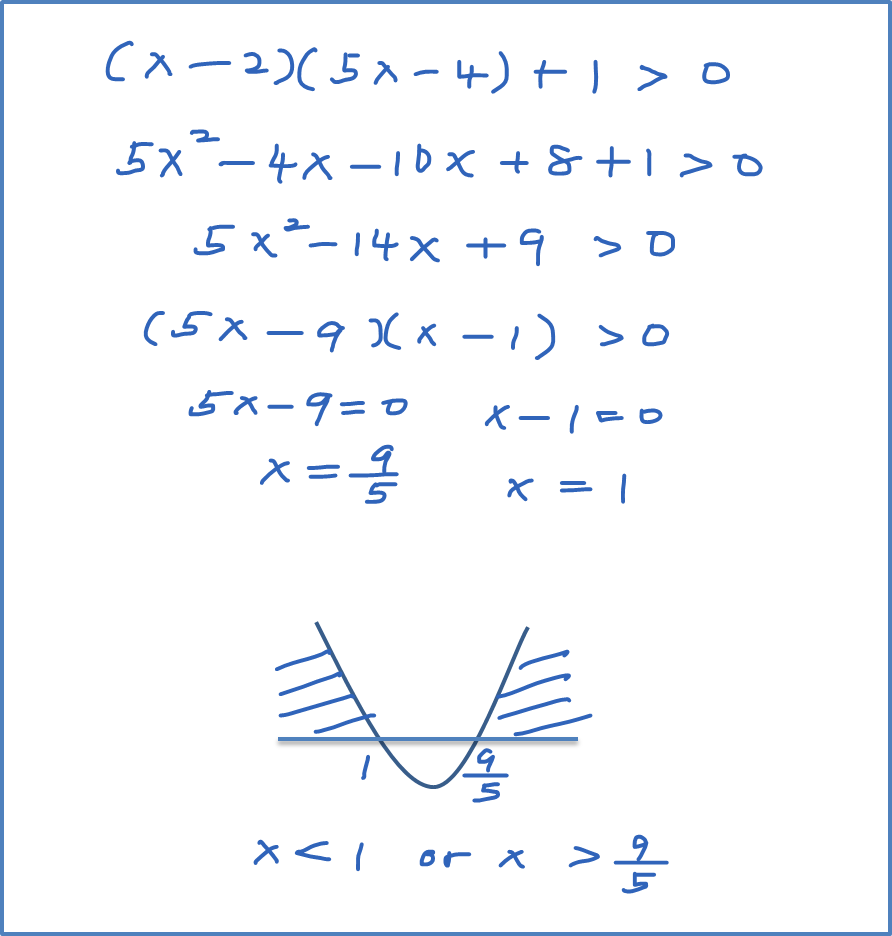
Write the quadratic inequality in standard form. We include the x-intercepts as the inequality The quadratic inequality in standard form.


 0 kommentar(er)
0 kommentar(er)
